Table of Contents
TogglePostulates of Boolean Algebra
There are several postulates of Boolean algebra in discreet mathematics. Imagine Boolean algebra postulates as the friendly guide in the world of Discrete Mathematics. They’re like your trusty map, showing the easiest routes through logical mazes. With these guides, you breeze through puzzles, making the journey of solving problems a fun and straightforward adventure. So all the postulates of Boolean algebra are as follow…
- Idempotent Law
- Commutative Law
- Associative Law
- Distributive Law
- Identity Element
- Complement or Negation
- De Morgan’s Laws
- Absorption Law
- Proof of some basic theorems
1. Idempotent Law
These laws are called “idempotent” because the result of Boolean variable remains the same, and it emphasizes that, if we are repeating the operation again and again, it doesn’t change the outcome. It is a important low of ” Postulates of Boolean Algebra”.
In simpler terms, if you AND (or OR) something with itself, you end up with the original thing or output. We can say that The Idempotent Law in Boolean algebra states that if you perform the AND operation or the OR operation of a variable with itself, the result is always the variable itself.
AND Idempotent Law
- Just imagine you have a statement, let’s call it ‘A’.
- If you combine ‘A’ with itself using AND, it’s like saying, “Is A true AND A true?” and than the result is just ‘A’ again.
- So, 👉 A AND A = A
OR Idempotent Law
- Now, if you take ‘A’ and combine it with itself using OR, it’s like asking, “Is A true OR A true?” The answer is still ‘A’ again.
So, 👉 A OR A = A
2. Commutative Law
The Commutative Law is a fundamental rule that applies to both the AND and OR operations in Boolean algebra ( It is a important low of ” Postulates of Boolean Algebra”).
commutative law is applicable only for addition and multiplication operations. But, it is not applied to other two arithmetic operations, such as subtraction and division.
It essentially states that the order in which you combine variables using these operations doesn’t affect the result. Means As per commutative laws or properties, if X and Y are any two integers, then the addition and multiplication of X and Y result in the same answer even if we change the position of X and Y.
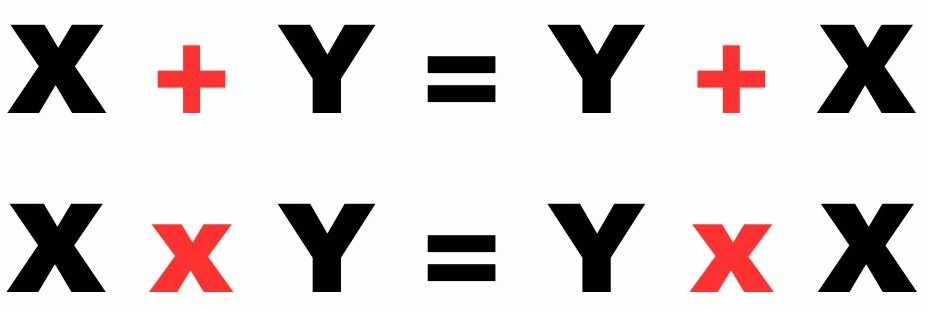
For example, if 5 and 6 are the two numbers, then;
5 + 6 = 6 + 5 = 11
5 × 6 = 6 × 5 = 30
AND Commutative Law
- If you have two variables, ‘A’ and ‘B,’ the AND Commutative Law states that A AND B is equivalent to B AND A.
- The order of combining doesn’t matter. The result is the same.
- Mathematically 👉 A AND B = B AND A
- For example, if ‘A’ represents “It’s sunny,” and ‘B’ represents “I am happy,” then “It’s sunny AND I am happy” is the same as “I am happy AND It’s sunny”.
- The outcome, in both cases, is the same — both conditions must be true (1) for the overall statement to be true (1).
OR Commutative Law
- Similarly, with the OR operation, the Commutative Law states that A OR B is the same as B OR A.
- It is important to note that the order of the variables in the OR operation doesn’t change the result.
- Mathematically: A OR B = B OR A
- For instance, if ‘A’ represents “It’s sunny,” and ‘B’ represents “I am inside,” then “It’s sunny OR I am inside” is equivalent to “I am inside OR It’s sunny.” In both cases, if either condition is true (1), the overall statement is true (1).
3. Associative Law
The Associative Law is like a rule for grouping things together in Boolean algebra. It tells us that, when we have more than two variables connected by the same operation (AND or OR), it doesn’t matter how we group them. whether you’re combining statements with AND or OR, you can group them in any way, and it won’t change the result. It’s like saying the way you group things with “and” or “or” doesn’t matter; the outcome stays the same. It is also a important low of ” Postulates of Boolean Algebra”.
The result will be the same. Means :-

AND Associative Law
- If you have three variables like, ‘A,’ ‘B,’ and ‘C,’ the AND Associative Law states that (A AND B) AND C is equivalent to A AND (B AND C).
- You can group them any way you like. The order of combining doesn’t change the result.
- Mathematically – (A❌ B) ❌ C = A ❌ (B ❌ C)
- The grouping doesn’t matter, both expressions have the same truth value.
OR Associative Law
- Similarly, in the OR operation, the Associative Law states that (A OR B) OR C is the same as A OR (B OR C).
- You can rearrange the grouping without changing the result.
- Mathematically -> (A + B) + C = A + (B + C)
- The grouping doesn’t affect the overall truth value.
4. Distributive Law
The Distributive Law in Boolean algebra is a powerful rule that describes how AND and OR operations interact when combined. Distributive property explains that, the operation performed on numbers, available in brackets that can be distributed for each number outside the brackets. It is one of the most frequently used properties in ” Postulates of Boolean Algebra”.
Let A, B and C are three different values than.
A ( B+ C) = AB + AC
There are two aspects to the Distributive Law that are as follow.
AND over OR (Distributive Law)
- The Distributive Law states that A AND (B OR C) is the same as
- (A AND B) OR (A AND C). or A ( B+ C) = AB + AC
In simple terms, it’s like saying if you want to AND a variable ‘A’ with a choice between ‘B’ or ‘C’ , it’s the same as ANDing ‘A’ with ‘B’ and then ORing it with ‘A’ AND ‘C’. This law distributes the AND operation over the OR operation.
OR over AND (Distributive Law)
- The Distributive Law also works the other way around. A OR (B AND C) is the same as (A OR B) AND (A OR C).
- Mathematically :- A OR (B AND C) = (A OR B) AND (A OR C)
- In simpler terms, if you want to OR a variable ‘A’ with the result of ANDing ‘B’ and ‘C,’ it’s the same as ORing ‘A’ with ‘B’ and then ANDing it with ‘A’ OR ‘C.’ This law distributes the OR operation over the AND operation.
5. Identity Element
The Identity Element is like a special guest or number that, when combined with another statement using AND or OR, doesn’t change anything. It’s like having a friend who, no matter what you do together, doesn’t affect the situation.
A OR 0 = A
A AND 1 = A
AND Identity Element (1)
- When you AND any statement ( A ) with ‘1’, it’s like saying, “Is ‘A’ true AND my special friend ‘1’ true?” The result is just ‘A’ — the special friend ‘1’ doesn’t alter or change the outcome or result.
- Mathematically: A AND 1 = A or A * 1 = 1.
OR Identity Element (0)
- When you OR any statement ( A ) with ‘0’ it’s like saying, “Is ‘A’ true OR my friendly number ‘0’ true?” The result is still ‘A’ — the friendly number ‘0’ doesn’t change the outcome.
- Mathematically: A OR 0 = A or A + 0 = A.
6. Complement or Negation
The complement or negation of a Boolean algebra or expression is a new expression that has the opposite truth value of the original expression. The complement of a variable or term is indicated by putting a bar or a tilde over it. It is also a important low of ” Postulates of Boolean Algebra”.
Example:-
- If A is a Boolean variable, then the complement of A is denoted as A’, ~A, or simply -A.
- The complement of a Boolean expression is also referred to as inverse or negation.
NOT Operation
- The NOT operation, or complement, is a way of flipping the truth (1) value of a statement. If ‘A’ is true (1), then NOT ‘A’ is false (0), and vice versa.
- Mathematically:- NOT A = A’
In Simple Terms
- Think of it as looking at the opposite side of a coin. If one side is true (heads), the complement (tails) is false, and vice versa. It is as simple as that.
- In everyday language, if ‘A’ is a true statement, NOT ‘A’ is the opposite or false.
Truth Table
- The truth table for the complement is straightforward. If ‘A’ is true, ‘A’ complement (NOT ‘A’) is false and if ‘A’ is false, ‘A’ complement is true.

Application
- Complement is often used to express the negation of a condition.
7. De Morgan’s Laws
De Morgan’s Laws are like rules that help when you’re working with groups of things called sets. They’re used in math to help with set operations like unions and intersections. It is a most important low of Postulates of Boolean Algebra.
There are two main rules of De Morgan’s Low that are as follow…
- The first rule says that if you combine two sets and then look at everything that’s not in that combined set, it’s the same as if you separately look at what’s not in each set and then put those things together.
- The second rule says that when you look at the things that are not in both sets combined, it’s the same as if you look at the things not in each set separately and then put all those things together.
De Morgan’s first law
De Morgan’s first law states that if you combine two sets and then look at everything that’s not in that combined set (called the complement), it’s the same as if you separately look at what’s not in each set and then put those things together. Mathematically, it’s written as:
The complement of the union of two sets (A and B) is equal to the intersection of their individual complements. Symbolically: (A ∪ B)’ = A’ ∩ B’
De Morgan’s second law
De Morgan’s second law in sets says that if you look at everything that’s not in both sets combined (called the complement of the intersection), it’s the same as if you separately look at what’s not in each set and then put all those things together. In symbols:
The complement of the intersection of two sets (A and B) is equal to the union of their individual complements. Symbolically: (A ∩ B)’ = A’ ∪ B’
De Morgan’s Law of Union
De Morgan’s Law of Union states that if you combine two sets (A and B) and then look at everything that’s not in that combined set (called the complement), it’s the same as separately looking at what’s not in each set and then putting those things together.
It can be represented as:
The complement of the union of two sets (A and B) is equal to the intersection of their individual complements. Symbolically: (A ∪ B)’ = A’ ∩ B’
De Morgan’s Law of Intersection
De Morgan’s Law of Intersection states that if you look at everything that’s not in both sets combined (called the complement of the intersection), it’s the same as separately looking at what’s not in each set and then putting all those things together.
It can be represented as:
The complement of the intersection of two sets (A and B) is equal to the union of their individual complements. Symbolically: (A ∩ B)’ = A’ ∪ B’
8. The Absorption Law
The Absorption Law is a principle in Boolean algebra that shows how certain operations with sets can simplify to become simpler expressions.
There are two forms of the Absorption Law:
1.X ∪ (X ∩ Y) = X: This means that the union of a set X with the intersection of X and another set Y is simply the set X itself. In simpler terms, if you combine a set with the part that it has in common with another set, you just get back the original set.
2.X ∩ (X ∪ Y) = X: This states that the intersection of a set X with the union of X and another set Y is also just the set X. In other words, when you find what’s common between a set and everything in another set, you end up with just the original set.

I am an Engineer and Passionate Blogger, who loves to share Deep, purified and Latest Information about IT (Information Technology) sector. Read More….

Leave a Reply