Table of Contents
ToggleBoolean Algebra
Boolean algebra is nothing but it just a mathematical structure or set of mathematical instructions that are used in digital circuit design, programming, and computer science.
It deals with binary variables and operations, where having only two possible values: true (1) or false (0), or we can say that, it always works on these two values 0 and 1.

History
George Boole (1815–1864): Boole was a British mathematician and logician. He is known as father of Boolean algebra. In 1847, he published a seminal work titled “The Mathematical Analysis of Logic,” where he laid the foundations for this algebraic system.
Claude Shannon (1916–2001): Claude Shannon was also a mathematician. In 1937, he was studying at MIT. He figured out that you could use this Boolean algebra stuff to make electrical circuits. It is a bit like using the rules of true and false to make things happen in electronics. This discovery was a important thing because it’s one of the reasons we have computers and cool electronic gadgets in our daily life. So, credit of Boolean Algebra also goes to Claud Shannon.

Key Concepts
1. Binary Variables
- In B A , we work with things that can either be true (like saying “yes”) or false (like saying “no”). These are the only two options such as true and false. true is represented as 1, and false is represented as 0.
2. Logical Operations
It generally uses four main operations to work with these two values that are true and false.
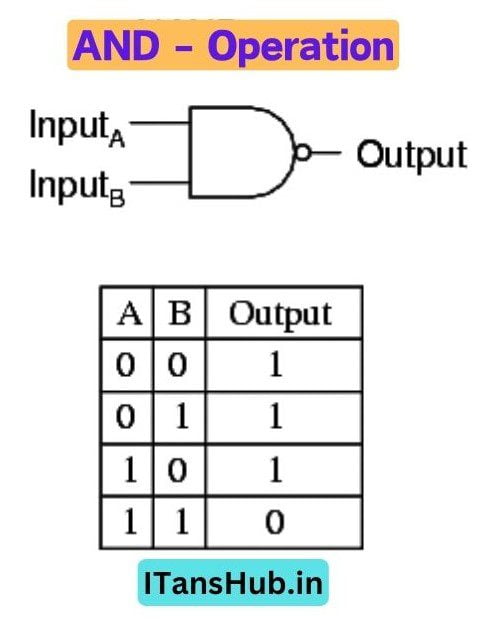
A. AND operation
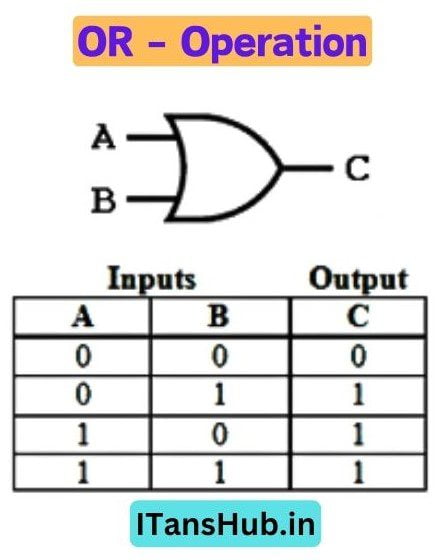
B. OR operation
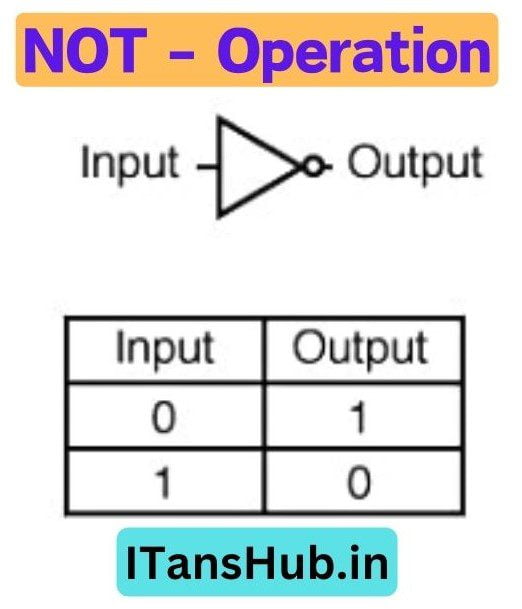
C. NOT operation
A. AND (Think of Multiplication)
- Imagine you have two things, let’s call them A and B.
- ANDing or multiplying A and B is like saying both A and B must be true for the result to be true.
- It is like saying, “Is it sunny AND am I happy?” If both are true, then the overall statement is true, Otherwise false.
- It is also known as Conjunction.
B. OR (Think of Addition)
- Picture having two things, A and B.
- ORing or Adding A and B is like saying at least one of them needs to be true for the result to be true, Otherwise false.
- For example, “Is it sunny OR am I inside?” If either is true, then the overall statement is true.
C. NOT (Think of Saying the Opposite)
- If something is true, NOT true makes it false, and if something is false, NOT false makes it true. Means it makes the value opposite.
- It’s like flipping the situation.
- It is also known as Negation.
D. Complement (A Little Extra)
- Complement is like the extra touch in B A.
- It involves taking the opposite of something. If you have a true statement, the complement is false, and. If you have a false statement, the complement is true.
3. Applications
It is like a tool. That is used in different areas such as:
- Computer Science: It helps computers make decisions based on true and false values.
- Digital Electronics: It’s used to design circuits in devices like computers, calculator and phones.
- Information Theory: It also helps in managing and processing information effectively.
FAQs
1. What is Boolean algebra with an example?
It is like a set of rules for dealing with true and false statements. Imagine you have two statements, such as A and B
AND (Multiplication) ➡️ A AND B is true only if both A and B are true.
Example:- Is it sunny AND am I happy? If both are true, the overall statement is true. Otherwise all statements are false.
OR (Addition) ➡️ A OR B is true if at least one of them is true.
Example: Is it sunny OR am I inside? If either is true, the overall statement is true. Otherwise all statements are false.
NOT (Opposite) ➡️ NOT A is the opposite of A’.
Example:- If “I am happy” is true, then “NOT I am happy” is false.
2. What is meant by a truth table?
A truth table is like a cheat sheet that shows all possible outcomes of a Boolean expression. It lists every combination of true and false for the variables involved and the result of the expression. It helps us see how different inputs affect the output, and it also help us to design circuits.
3. What are the types of Boolean algebra?
There are different types of Boole.. algebra, but there are only two main types are as follow :-
- Binary B-Algebra: Deals with variables having only two possible values, true (1) and false (0).
- Multivalued B- Algebra: Allows variables to have more than two values.
4. Are B- Algebra and Discrete Mathematics the same or different?
They are related to each other but not exactly the same. B- algebra is a part of discrete mathematics. Discrete mathematics is a broader field that includes various topics like logic, sets, and relations. B- algebra specifically focuses on dealing with true and false values and logical operations. So B- Algebra and Discreet Mathematics are slightly different.
5. Where is B- algebra used?
It is generally used in various areas, such as:-
- Computer Science: In designing computer circuits and programming logics.
- Digital Electronics: For creating digital circuits and systems.
- Information Theory: In fields related to data transmission and storage.

I am an Engineer and Passionate Blogger, who loves to share Deep, purified and Latest Information about IT (Information Technology) sector. Read More….

Leave a Reply